# RNN and LSTM

# RNN

link 内容来源如下 仅总结以及个人笔记 （叠甲）

1. 如何从 RNN 起步，一步一步通俗理解 LSTM_rnn lstm-CSDN 博客
2. Understanding LSTM Networks – colah’s blog
3. 大白话：我不信看完这篇文章，你还不懂 LSTM - 知乎

# RNN Recurrent Neural Networks

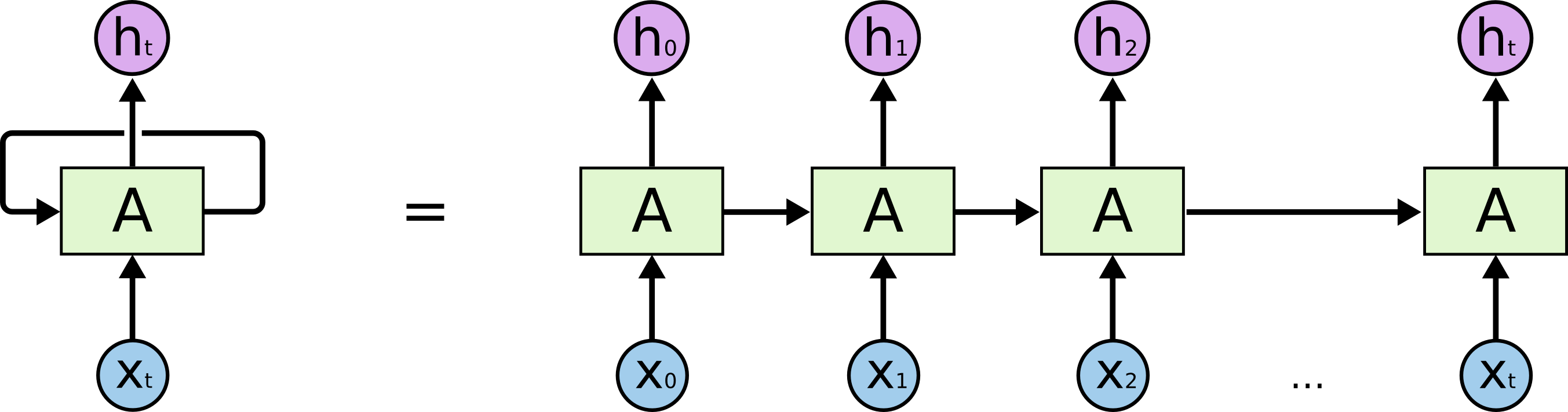
x0, x1, x2,… 为时间序列，h0, h1, h2,… 为每一步的隐藏层，则有：

$$h_t = f(Ux_t + Wh_{t-1} + b)$$

1. 当前隐藏层 ht 由上一步的隐藏层 ht-1 与当前步的输入 xt 共同决定
2. 每一步计算的 W，U 参数共享
3. 实际中 ht 一般只包含前面若干步而非之前所有步的隐藏状态

# RNN 的局限：长期依赖（Long-TermDependencies）问题

间隔不断增大时，RNN 会丧失学习到连接如此远的信息的能力。例如试着去预测 “I grew up in France…I speak fluent French” 最后的词 “French”。当前的信息建议下一个词可能是一种语言的名字，但是如果我们需要弄清楚是什么语言，我们是需要先前提到的离当前位置很远的 “France” 的上下文。这说明相关信息和当前预测位置之间的间隔就肯定变得相当的大。RNN 会受到短时记忆的影响。如果一条序列足够长，那它们将很难将信息从较早的时间步传送到后面的时间步。

# LSTM Long Short Term Memory networks

长短期记忆网络 —— 通常简称为 “LSTM”—— 是一种特殊的循环神经网络，能够学习长期依赖关系，它们由 Hochreiter & Schmidhuber (1997) 引入，并在后续工作中被许多人改进和推广。 1 它们在各种问题上表现极好，现在被广泛使用。

LSTM 的 “记忆” 我们叫做细胞 /cells，你可以直接把它们想做黑盒，这个黑盒的输入为前状态 ht-1 和当前输入 xt。这些 “细胞” 会决定哪些之前的信息和状态需要保留 / 记住，而哪些要被抹去。实际的应用中发现，这种方式可以有效地保存很长时间之前的关联信息，例如当你浏览评论时，你的大脑下意识地只会记住重要的关键词，比如 “amazing” 和 “awsome” 这样的词汇，而不太会关心 “this”、“give”、“all”、“should” 等字样。如果朋友第二天问你用户评价都说了什么，那你可能不会一字不漏地记住它，而是会说出但大脑里记得的主要观点，比如 “下次肯定还会来买”，那其他一些无关紧要的内容自然会从记忆中逐渐消失。

RNN 都具有一种重复神经网络模块的链式的形式。在标准的 RNN 中，这个重复的模块只有一个非常简单的结构，例如一个 tanh 层。

LSTM 同样是这样的结构，但是重复的模块拥有一个不同的结构。具体来说，RNN 是重复单一的神经网络层，LSTM 中的重复模块则包含四个交互的层，三个 Sigmoid 和一个 tanh 层，并以一种非常特殊的方式进行交互。

上图中，σ 表示的 Sigmoid 激活函数与 tanh 函数类似，不同之处在于 sigmoid 是把值压缩到 0~1 之间而不是 -1~1 之间。这样的设置有助于更新或忘记信息，相当于要么是 1 则记住，要么是 0 则忘掉，所以还是这个原则：因记忆能力有限，记住重要的，忘记无关紧要的。

# 核心思想

LSTM 的关键就是细胞状态，水平线在图上方贯穿运行。细胞状态类似于传送带。直接在整个链上运行，只有一些少量的线性交互。信息在上面流传保持不变会很容易。

LSTM 有通过精心设计的称作为 “门” 的结构来去除或者增加信息到细胞状态的能力。门是一种让信息选择式通过的方法。他们包含一个 sigmoid 神经网络层和一个 pointwise 乘法的非线性操作。

LSTM 拥有三种类型的门结构：遗忘门 / 忘记门、输入门和输出门，来保护和控制细胞状态。

1. 遗忘门

   LSTM 中的第一步是决定我们会从细胞状态中丢弃什么信息。这个决定通过一个称为 “忘记门” 的结构完成。该忘记门会读取上一个输出 ht-1 和当前输入 xt，做一个 Sigmoid 的非线性映射，然后输出一个向量 ft（该向量每一个维度的值都在 0 到 1 之间，1 表示完全保留，0 表示完全舍弃，相当于记住了重要的，忘记了无关紧要的），最后与细胞状态 Ct-1 相乘。

   $$f_t=\sigma(W_f[H_{t-1},x_t] + b_f)$$

2. 输入门

   确定什么样的新信息被存放在细胞状态中

3. 细胞状态

   旧状态$C_{t-1}$ 与$f_t$ 相乘，丢弃掉我们确定需要丢弃的信息，接着加上$i_t * C_t$。这就是新的候选值，根据我们决定更新每个状态的程度进行变化

4. 输出门

   最终，我们需要确定输出什么值。这个输出将会基于我们的细胞状态，但是也是一个过滤后的版本。

   • 首先，我们运行一个 sigmoid 层来确定细胞状态的哪个部分将输出出去。
   • 接着，我们把细胞状态通过 tanh 进行处理（得到一个在 - 1 到 1 之间的值）并将它和 sigmoid 门的输出相乘，最终我们仅仅会输出我们确定输出的那部分。
   • 在语言模型的例子中，因为他就看到了一个代词，可能需要输出与一个动词相关的信息。例如，可能输出是否代词是单数还是负数，这样如果是动词的话，我们也知道动词需要进行的词形变化，进而输出信息。

5. 注意

   $W_f$，在不同的 LSTM cell 是共享的，不同门之间有$W_f$，$W_i$，$W_c$，$W_o$，则不共享 (见引用 3)

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90

   # LSTM import math from typing import Tuple from matplotlib import pyplot as plt import torch import torch.nn as nn import torch.optim as optim import numpy as np def init_weights(weight,hidden_size): stdv = 1.0 / math.sqrt(hidden_size) weight.data.uniform_(-stdv, stdv) return weight class LSTM(nn.Module): def __init__(self, input_sz: int, hidden_sz: int, output_sz): """ :param: input_sz = m :param: hidden_sz = n :param: output_sz = 3 """ super().__init__() self.input_size = input_sz self.hidden_size = hidden_sz #f_t self.U_f = nn.Parameter(torch.Tensor(input_sz, hidden_sz)) #链接输入x_t和上一层隐藏层h_{t-1}, mxn self.V_f = nn.Parameter(torch.Tensor(hidden_sz, hidden_sz)) #全链接上一层隐藏层h_{t-1}和这一层隐藏层h_t, nxn self.b_f = nn.Parameter(torch.Tensor(hidden_sz)) #bias项，链接向量1和这一层隐藏层h_t, nx1 #i_t self.U_i = nn.Parameter(torch.Tensor(input_sz, hidden_sz)) #链接输入x_t和上一层隐藏层h_{t-1}, mxn self.V_i = nn.Parameter(torch.Tensor(hidden_sz, hidden_sz)) #链接上一层隐藏层h_{t-1}和这一层隐藏层h_t, nxn self.b_i = nn.Parameter(torch.Tensor(hidden_sz)) #bias项，链接向量1和这一层隐藏层h_t, nx1 #c_t self.U_c = nn.Parameter(torch.Tensor(input_sz, hidden_sz)) #链接输入x_t和上一层隐藏层h_{t-1}, mxn self.V_c = nn.Parameter(torch.Tensor(hidden_sz, hidden_sz)) #链接上一层隐藏层h_{t-1}和这一层隐藏层h_t, nxn self.b_c = nn.Parameter(torch.Tensor(hidden_sz)) #bias项，链接向量1和这一层隐藏层h_t, nx1 #o_t self.U_o = nn.Parameter(torch.Tensor(input_sz, hidden_sz)) #链接输入x_t和上一层隐藏层h_{t-1}, mxn self.V_o = nn.Parameter(torch.Tensor(hidden_sz, hidden_sz)) #链接上一层隐藏层h_{t-1}和这一层隐藏层h_t, nxn self.b_o = nn.Parameter(torch.Tensor(hidden_sz)) #bias项，链接向量1和这一层隐藏层h_t, nx1 # init weights self.U_f = init_weights(self.U_f,hidden_sz) self.V_f = init_weights(self.V_f,hidden_sz) self.b_f = init_weights(self.b_f,hidden_sz) self.U_i = init_weights(self.U_i,hidden_sz) self.V_i = init_weights(self.V_i,hidden_sz) self.b_i = init_weights(self.b_i,hidden_sz) self.U_c = init_weights(self.U_c,hidden_sz) self.V_c = init_weights(self.V_c,hidden_sz) self.b_c = init_weights(self.b_c,hidden_sz) self.U_o = init_weights(self.U_o,hidden_sz) self.V_o = init_weights(self.V_o,hidden_sz) self.b_o = init_weights(self.b_o,hidden_sz) # output self.fcn = nn.Linear(hidden_sz, output_sz) #全连接矩阵，链接最后一层隐藏层h_T和输出y, nxoutput def forward(self,x): """ assumes x.shape represents (batch_size, time_step, num_feature) batch_size不用管，因为我们不会只传一条时序进来，基本传比如100个相同规律的 时序进来，那么batch_size=100，反正torch计算可以对整个batch运算 """ bs, ts, _ = x.size() # batch size, time step h_t = torch.zeros(bs, self.hidden_size) c_t = torch.zeros(bs, self.hidden_size) for t in range(ts): #时间步长为T x_t = x[:, t, :] f_t = torch.sigmoid(x_t @ self.U_f + h_t @ self.V_f + self.b_f) i_t = torch.sigmoid(x_t @ self.U_i + h_t @ self.V_i + self.b_i) c_tilde_t = torch.tanh(x_t @ self.U_c + h_t @ self.V_c + self.b_c) o_t = torch.sigmoid(x_t @ self.U_o + h_t @ self.V_o + self.b_o) c_t = f_t * c_t + i_t * c_tilde_t # dot product, dot add h_t = o_t * torch.tanh(c_t) # dot product # empty dimension at 0, [1,time_step,hidden_num] y = self.fcn(h_t) # 最后一个隐藏层输出 return y # [batch_size x num_output]